COMPLEMENTOS
FÓRMULAS E MAPAS ÚTEIS
DISTRIBUIÇÃO DE WEIBULL
A Distribuição Estatística de Weibull[82] é definida por dois parâmetros: um de escala (C, em m/s) e outro de forma (k, adimensional). A frequência de ocorrência de uma velocidade u é demonstrada matematicamente por
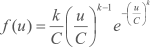
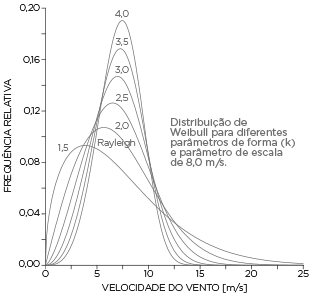
Na FIGURA D.1 é apresentada a distribuição de Weibull para diferentes fatores de forma. No caso do fator de forma ser igual a 2, deriva-se a Distribuição de Rayleigh, caracterizada apenas pelo fator de escala (C, em m/s), que representa, neste caso, a velocidade média do vento[82]
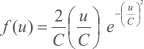
Por ser mais geral, a Distribuição de Weibull apresenta melhor aderência às estatísticas de velocidade do vento, uma vez que o fator de forma pode assumir valores bastante superiores a 2[4].
A função densidade de probabilidade cumulativa, F(u), associada à probabilidade da velocidade do vento ser maior que u, expressa-se por
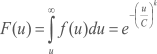
O valor médio ou valor esperado da velocidade do vento é dado por
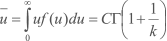
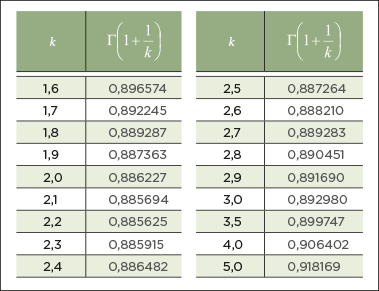
em que a Função Gama (Γ) é definida por
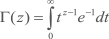
A Tabela D.1 apresenta a Função Gama para diversos valores de k.
O Fluxo ou Densidade de Potência Eólica é definido como
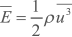 (W/m²)
(W/m²)
que, expressando-se em termos da distribuição de Weibull, resulta em
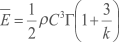 (W/m²)
(W/m²)
em que ρ é a densidade do ar[65].A FIGURA D.2 apresenta exemplos da variação do fluxo de potência eólica em função da velocidade do vento e do fator de forma de Weibull.
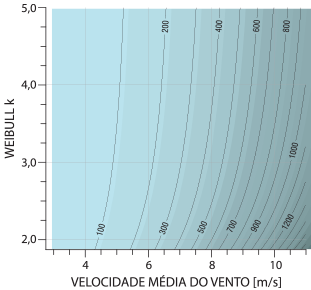
O GRÁFICO C.2 apresenta a correspondência entre o fluxo de potência eólica e a velocidade média do vento, para diferentes fatores de forma de Weibull.
Em condições neutras de estratificação térmica vertical da atmosfera, o perfil de velocidade vertical do vento na camada-limite pode ser aproximado pela Lei Logarítmica segundo a relação[77]
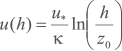
onde u(h) é a velocidade do vento na altura h, z0 é a rugosidade do terreno, 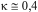 é a constante de Von Kármán e u* é a velocidade de atrito[85].
é a constante de Von Kármán e u* é a velocidade de atrito[85].
Escrevendo-se a Lei Logarítmica para representar a velocidade do vento em duas alturas h1 e h2, e dividindo-se uma expressão pela outra, pode-se relacionar as velocidades do vento em duas alturas:
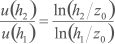
Explicitando-se a rugosidade dessa expressão, tem-se
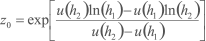
A variação vertical da velocidade do vento na camada-limite também pode ser expressa em termos da Lei de Potência, segundo a relação
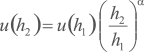
onde u(h) é a velocidade do vento na altura h e α é o “expoente de camada-limite”.
Desta relação, pode-se explicitar o expoente de camada-limite – α em função das velocidades de vento em duas alturas, resultando em
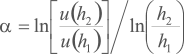
DENSIDADE DO AR
A potência gerada por uma turbina eólica é função direta da densidade do ar que impulsiona o rotor. As curvas de potência fornecidas pelos fabricantes são usualmente dadas para condições padrão da atmosfera (15 °C, nível do mar, densidade do ar de 1,225 kg/m³). Portanto, o desempenho das máquinas nas diversas condições de operação deve ser corrigido para o efeito da variação da densidade com a altitude e a temperatura locais. No Capítulo 6 foi apresentado o MAPA DE DENSIDADE MÉDIA ANUAL DO AR para todo o Estado da Paraíba, considerando-se um perfil vertical de temperatura segundo as equações da Atmosfera Padrão Internacional – ISA[68], calculado sobre o modelo de relevo na resolução de 100 m x 100 m e ajustado para dados de temperatura coletados em estações do INMET, entre 1961 e 1990[42].
Uma expressão aproximada para o cálculo da densidade do ar ρ (em kg/m³) a partir da temperatura T (em °C) e altitude z (em metros) é dada por:
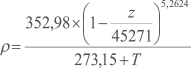
ESTEIRA AERODINÂMICA
Uma turbina eólica capta uma parte da energia cinética do vento, que passa através da área varrida pelo rotor, e a transforma em energia elétrica. A potência elétrica é função do cubo da velocidade de vento v:
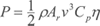 (Watts)
(Watts)
em que Ar é a área varrida pelo rotor, Cp é o coeficiente aerodinâmico de potência do rotor (valor máximo teórico = 0,593, na prática atinge 0,45 e é variável com vento, rotação, e parâmetros de controle da turbina) e η é a eficiência do conjunto gerador/transmissões mecânicas e elétricas (~0,93-0,98).
Ao absorver a energia cinética, o rotor reduz a velocidade do vento imediatamente a sotavento do disco, mas essa velocidade se recupera gradualmente, ao se misturar com as massas de ar do escoamento livre. Após alguma distância a sotavento, que varia com a velocidade do vento, com a condição de operação da turbina, com a rugosidade de terreno e com a condição de estabilidade térmica da atmosfera, o escoamento praticamente recupera a velocidade original e turbinas adicionais podem ser instaladas. A relação entre as velocidades do escoamento livre (u0) e na esteira, a uma distância axial x do rotor (u), é dada por[44]
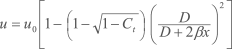
sendo
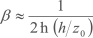 e
e 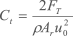
PRODUÇÃO ANUAL DE ENERGIA (PAE) E FATOR DE CAPACIDADE
A Produção Anual de Energia – PAE de uma turbina eólica pode ser calculada pela integração das curvas de potência (P(u), em kW) e da frequência de ocorrência das velocidades de vento (f(u))[44].
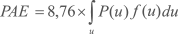 (MWh)
(MWh)
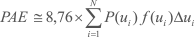 (MWh)
(MWh)
O “fator de capacidade” é definido como a razão entre a energia efetivamente gerada e a energia teórica que seria gerada considerando-se a potência nominal (Pn) do aerogerador:
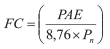
CUSTO DE GERAÇÃO
A expressão a seguir é uma fórmula prática para se estimar o custo médio de geração ao longo da vida útil de um empreendimento eólico:
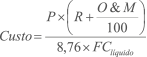 (R$/MWH)
(R$/MWH)
onde:
P = investimento inicial (R$/kW)
R = rendimento do investimento
O&M = custo percentual esperado das despesas com operação e manutenção em relação ao investimento total. Pode-se utilizar como valor de referência: O&M= 2%.
FC líquido = fator de capacidade líquido da usina
Na fórmula anterior, o fator R (rendimento) pode ser calculado da seguinte maneira:
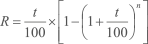
onde:
t = taxa de atratividade (%/ano)
n = vida útil da usina (anos)
E o fator de capacidade líquido pode ser calculado por:
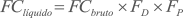
onde:
FCbruto = fator de capacidade bruto da usina
FD = fator de disponibilidade; pode-se utilizar como valor de referência FD = 0,97
FP = fator resultante de outras perdas, como perdas elétricas no sistema de distribuição. Pode-se utilizar como valor de referência: FP = 0,96
Na equação anterior, o fator de capacidade bruto da usina é dado por:

onde:
E = produção anual de energia bruta estimada para a usina (MWh)
Pot = capacidade instalada total da usina (MW)
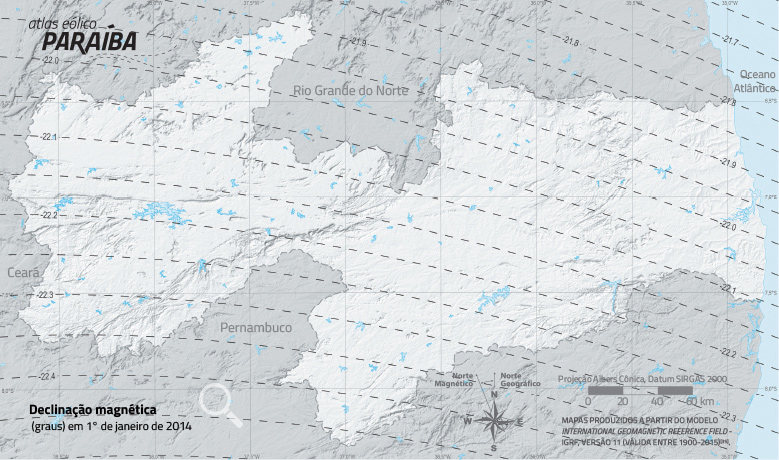
DECLINAÇÃO MAGNÉTICA
Como informação auxiliar à instalação futura de sensores de direção em torres anemométricas no Estado da Paraíba, foram desenvolvidos mapas de declinação magnética e variação magnética anual para os anos de 2011-2015[35].